Soft Margin Support Vector Machine
Welcome to the 31st part of our machine learning tutorial series and the next part in our Support Vector Machine section. In this tutorial, we're going to talk about the Soft Margin Support Vector Machine.
First, there are two major reasons why the soft-margin classifier might be superior. One reason is your data is not perfectly linearly separable, but is very close and it makes more sense to continue using the default linearly kernel. The other reason is, even if you are using a kernel, you may wind up with significant over-fitment if you want to use a hard-margin. For example, consider:
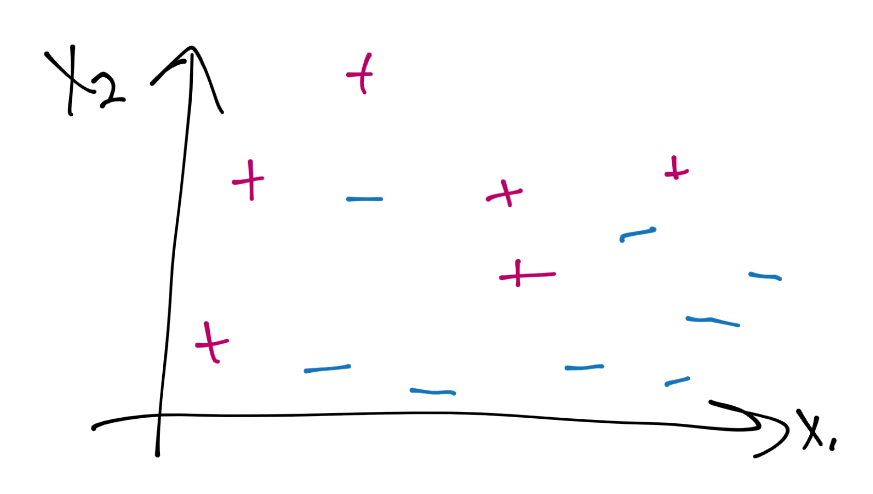
Here's a case of data that isn't currently linearly separable. Assuming a hard-margin (which is what we've been using in our calculations so far), we might use a kernel to achieve a decision boundary of:
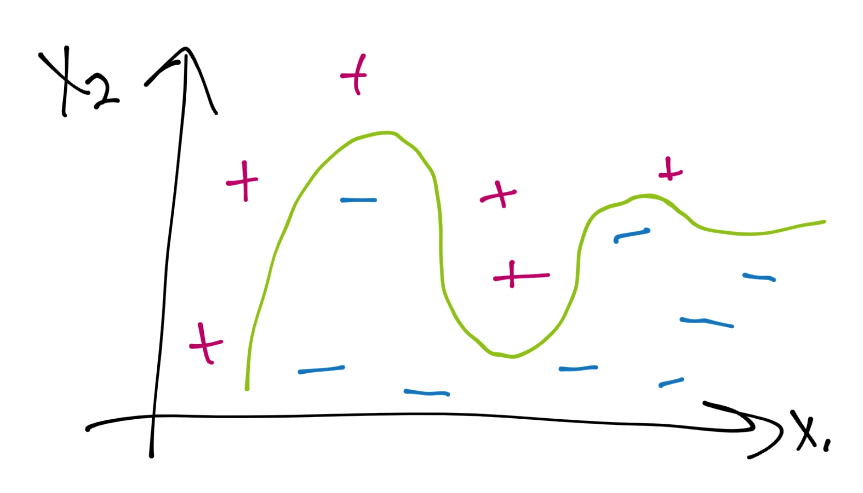
Next, noting imperfections in my drawing abilities, let's draw the support vector hyperplanes, and circle the support vectors:
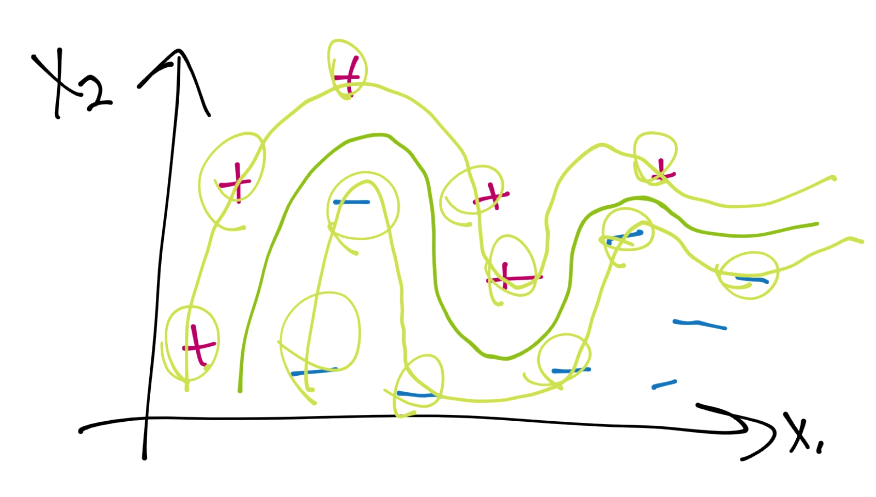
In this case, every single data sample for the positive class is a support vector, and only two of the negative class aren't support vectors. This signals to use a high chance of overfitting having happened. That's something we want to avoid, since, as we move forward to classify future points, we have almost no wiggle room, and are likely to miss-classify new data. What if we did something like this instead:
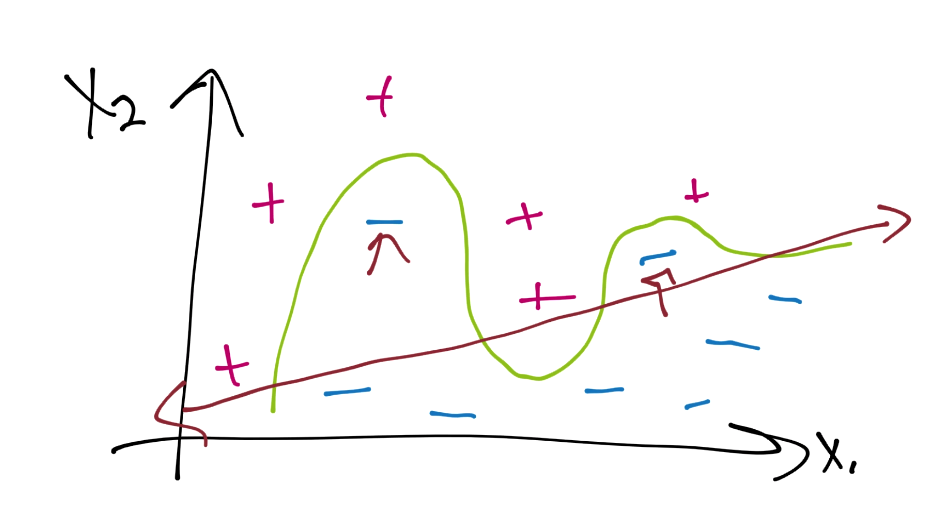
We have a couple errors or violations noted by arrows, but this is likely to classify future featuresets better overall. What we have here is a "soft margin" classifier, which allows for some "slack" on the errors that we might get in the optimization process.
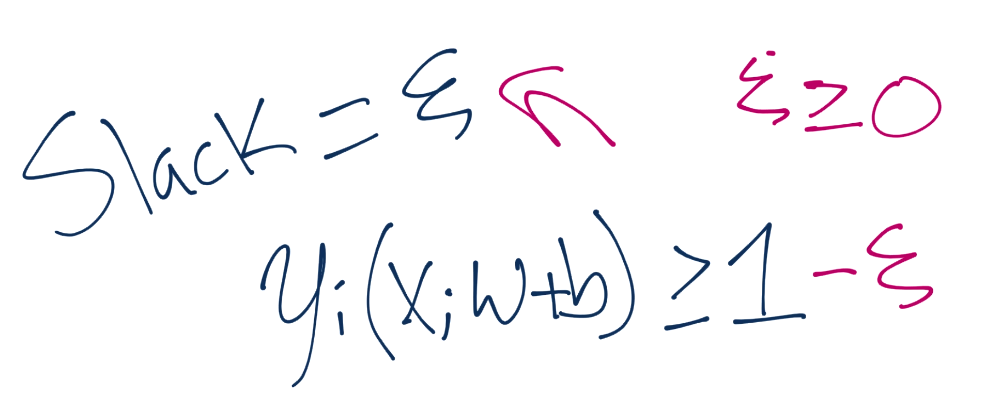
Our new optimization is the above calculation, where slack is greater than or equal to zero. The closer to 0 the slack is, the more "hard-margin" we are. The higher the slack, the more soft the margin is. If slack was 0, then we'd have a typical hard-margin classifier. As you might guess, however, we'd like to ideally minimize slack. To do this, we add it to the minimization of the magnitude of vector w:
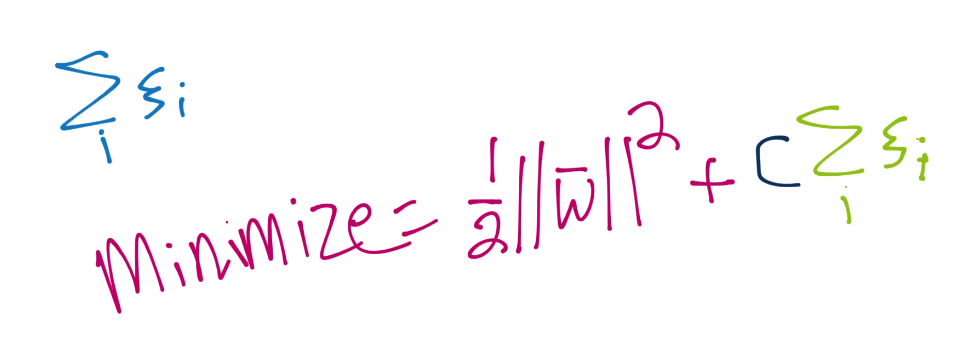
Thus, we actually want to minimize 1/2||w||^2 + (C * The sum of all of the slacks used).With that, we brough in yet another variable, C. C is a multiplier for the "value" of how much we want slack to affect the rest of the equation. The lower C, the less important the sum of the slacks is in relation to the magnitude of vector w, and visa versa. In most cases, C will be defaulted to 1.
So there you have the Soft-Margin Support Vector Machine, and why you might want to use it. Next, we're going to show some sample code that incorporates a soft margin, kernels, and CVXOPT.
-
Practical Machine Learning Tutorial with Python Introduction
-
Regression - Intro and Data
-
Regression - Features and Labels
-
Regression - Training and Testing
-
Regression - Forecasting and Predicting
-
Pickling and Scaling
-
Regression - Theory and how it works
-
Regression - How to program the Best Fit Slope
-
Regression - How to program the Best Fit Line
-
Regression - R Squared and Coefficient of Determination Theory
-
Regression - How to Program R Squared
-
Creating Sample Data for Testing
-
Classification Intro with K Nearest Neighbors
-
Applying K Nearest Neighbors to Data
-
Euclidean Distance theory
-
Creating a K Nearest Neighbors Classifer from scratch
-
Creating a K Nearest Neighbors Classifer from scratch part 2
-
Testing our K Nearest Neighbors classifier
-
Final thoughts on K Nearest Neighbors
-
Support Vector Machine introduction
-
Vector Basics
-
Support Vector Assertions
-
Support Vector Machine Fundamentals
-
Constraint Optimization with Support Vector Machine
-
Beginning SVM from Scratch in Python
-
Support Vector Machine Optimization in Python
-
Support Vector Machine Optimization in Python part 2
-
Visualization and Predicting with our Custom SVM
-
Kernels Introduction
-
Why Kernels
-
Soft Margin Support Vector Machine
-
Kernels, Soft Margin SVM, and Quadratic Programming with Python and CVXOPT
-
Support Vector Machine Parameters
-
Machine Learning - Clustering Introduction
-
Handling Non-Numerical Data for Machine Learning
-
K-Means with Titanic Dataset
-
K-Means from Scratch in Python
-
Finishing K-Means from Scratch in Python
-
Hierarchical Clustering with Mean Shift Introduction
-
Mean Shift applied to Titanic Dataset
-
Mean Shift algorithm from scratch in Python
-
Dynamically Weighted Bandwidth for Mean Shift
-
Introduction to Neural Networks
-
Installing TensorFlow for Deep Learning - OPTIONAL
-
Introduction to Deep Learning with TensorFlow
-
Deep Learning with TensorFlow - Creating the Neural Network Model
-
Deep Learning with TensorFlow - How the Network will run
-
Deep Learning with our own Data
-
Simple Preprocessing Language Data for Deep Learning
-
Training and Testing on our Data for Deep Learning
-
10K samples compared to 1.6 million samples with Deep Learning
-
How to use CUDA and the GPU Version of Tensorflow for Deep Learning
-
Recurrent Neural Network (RNN) basics and the Long Short Term Memory (LSTM) cell
-
RNN w/ LSTM cell example in TensorFlow and Python
-
Convolutional Neural Network (CNN) basics
-
Convolutional Neural Network CNN with TensorFlow tutorial
-
TFLearn - High Level Abstraction Layer for TensorFlow Tutorial
-
Using a 3D Convolutional Neural Network on medical imaging data (CT Scans) for Kaggle
-
Classifying Cats vs Dogs with a Convolutional Neural Network on Kaggle
-
Using a neural network to solve OpenAI's CartPole balancing environment
