Kernels Introduction
Welcome to the 29th part of our machine learning tutorial series and the next part in our Support Vector Machine section. In this tutorial, we're going to talk about the concept of kernels with machine learning.
Recall back in the very beginning on the topic of the Support Vector Machine our question about whether or not you could use an SVM with data like:
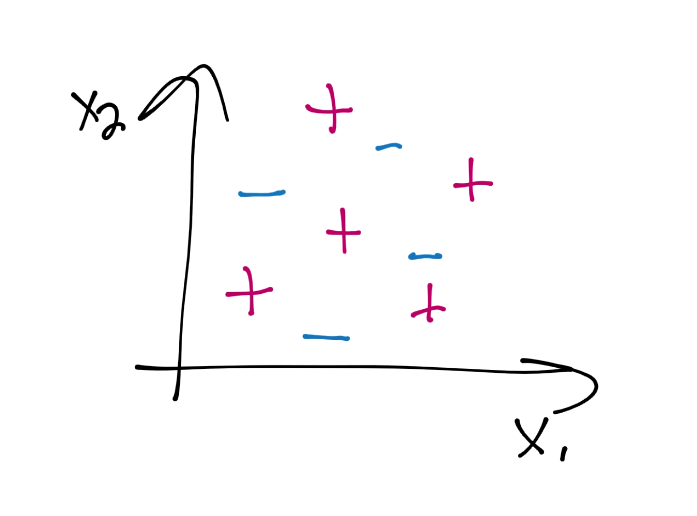
At least with what we know so far, is it possible? No, it is not, at least not like this. One option, however, is to take a new perspective. One can do this by adding a new dimension. For example with the data above, we could add a 3rd dimension using some sort of function. Something like X3 = X3 = X1*X2. That might work here, but, it may not. Also, what about in cases like with image analysis, where you might have hundreds, or more, dimensions? It's already the case that performance is an issue, and, should you need to add a bunch more dimensions to data that is already highly dimensional, we're only going to further significantly slow things down.
What if I told you that you could do calculations in plausibly infinite dimensions, or, better yet, you could have those calculations done for you in those dimensions, without you needing to work within those dimensions and still get the result back?
It turns out, that we actually can do this with what are known as Kernels. Many people first come into contact, and maybe lastly too, with kernels with respect to the Support Vector Machine. This could lead to thinking that kernels are mainly for use with Support Vector Machines, but this is actually not the case.
Kernels are similarity functions, which take two inputs and return a similarity using inner products. Since this is a machine learning tutorial, some of you might be wondering why people don't use kernels for machine learning algorithms, and, I am here to tell you that they do! Not only can you create your own new machine learning algorithms with Kernels, you can also translate existing machine learning algorithms into using Kernels.
What kernels are going to allow us to do, possibly, is work in many dimensions, without actually paying the processing costs to do it. Kernels do have a requirement: They rely on inner products. For the purposes of this tutorial, "dot product" and "inner product" are entirely interchangeable.
What we need to do in order to verify whether or not we can get away with using kernels is confirm that every interaction with our featurespace is an inner product. We'll start at the end, and work our way back to confirm this.
First, how did we determine classification of a featureset after training?

Is that interaction an inner product? Sure is! We can interchange vector x with vector z:
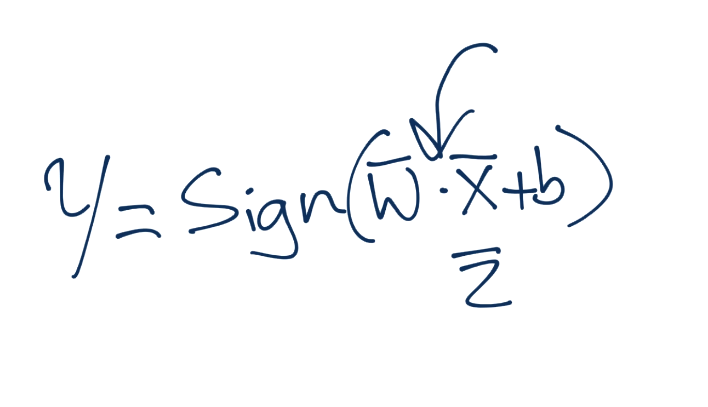
Moving along, we're going to revisit our constraints. Recall the constraint equation:
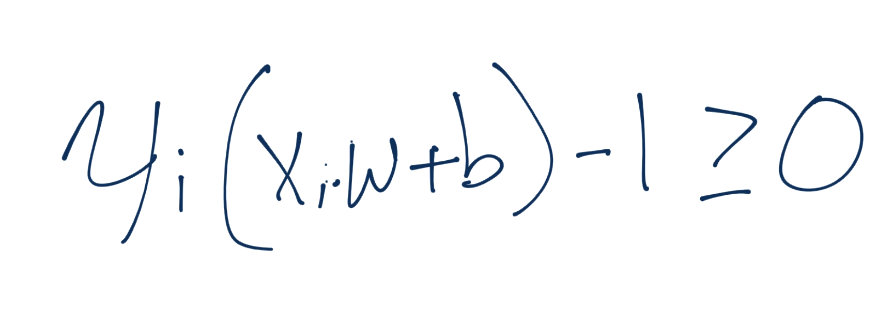
How about here? Is the interaction an inner product? Yes! Recall that yi(xi.w+b)-1 >= 0 is identical to yi(xi.w+b) >= 1. So here we can easily replace our x-sub-i value with our new z-sub-i.
Finally, what about the other formal optimization equation for w?

There's yet another dot product/inner product! Any other equations? How about:
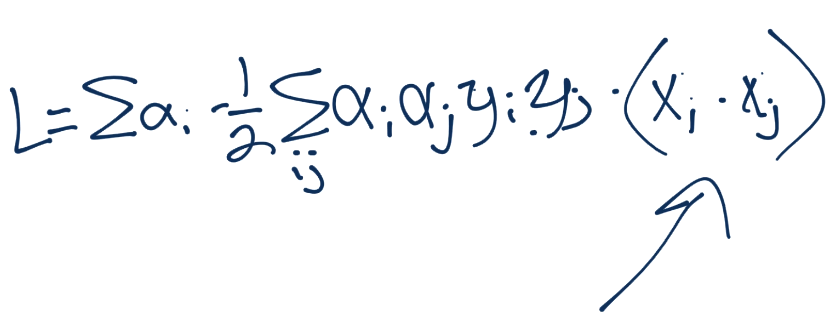
All good! Awesome, we can use Kernels. You're probably sitting there wondering though, what about this whole "calculations in infinite dimensions for free thing?" Well, first we needed to make sure we could do it. As for the free processing, you'll have to stick around until the next tutorial to get that!
-
Practical Machine Learning Tutorial with Python Introduction
-
Regression - Intro and Data
-
Regression - Features and Labels
-
Regression - Training and Testing
-
Regression - Forecasting and Predicting
-
Pickling and Scaling
-
Regression - Theory and how it works
-
Regression - How to program the Best Fit Slope
-
Regression - How to program the Best Fit Line
-
Regression - R Squared and Coefficient of Determination Theory
-
Regression - How to Program R Squared
-
Creating Sample Data for Testing
-
Classification Intro with K Nearest Neighbors
-
Applying K Nearest Neighbors to Data
-
Euclidean Distance theory
-
Creating a K Nearest Neighbors Classifer from scratch
-
Creating a K Nearest Neighbors Classifer from scratch part 2
-
Testing our K Nearest Neighbors classifier
-
Final thoughts on K Nearest Neighbors
-
Support Vector Machine introduction
-
Vector Basics
-
Support Vector Assertions
-
Support Vector Machine Fundamentals
-
Constraint Optimization with Support Vector Machine
-
Beginning SVM from Scratch in Python
-
Support Vector Machine Optimization in Python
-
Support Vector Machine Optimization in Python part 2
-
Visualization and Predicting with our Custom SVM
-
Kernels Introduction
-
Why Kernels
-
Soft Margin Support Vector Machine
-
Kernels, Soft Margin SVM, and Quadratic Programming with Python and CVXOPT
-
Support Vector Machine Parameters
-
Machine Learning - Clustering Introduction
-
Handling Non-Numerical Data for Machine Learning
-
K-Means with Titanic Dataset
-
K-Means from Scratch in Python
-
Finishing K-Means from Scratch in Python
-
Hierarchical Clustering with Mean Shift Introduction
-
Mean Shift applied to Titanic Dataset
-
Mean Shift algorithm from scratch in Python
-
Dynamically Weighted Bandwidth for Mean Shift
-
Introduction to Neural Networks
-
Installing TensorFlow for Deep Learning - OPTIONAL
-
Introduction to Deep Learning with TensorFlow
-
Deep Learning with TensorFlow - Creating the Neural Network Model
-
Deep Learning with TensorFlow - How the Network will run
-
Deep Learning with our own Data
-
Simple Preprocessing Language Data for Deep Learning
-
Training and Testing on our Data for Deep Learning
-
10K samples compared to 1.6 million samples with Deep Learning
-
How to use CUDA and the GPU Version of Tensorflow for Deep Learning
-
Recurrent Neural Network (RNN) basics and the Long Short Term Memory (LSTM) cell
-
RNN w/ LSTM cell example in TensorFlow and Python
-
Convolutional Neural Network (CNN) basics
-
Convolutional Neural Network CNN with TensorFlow tutorial
-
TFLearn - High Level Abstraction Layer for TensorFlow Tutorial
-
Using a 3D Convolutional Neural Network on medical imaging data (CT Scans) for Kaggle
-
Classifying Cats vs Dogs with a Convolutional Neural Network on Kaggle
-
Using a neural network to solve OpenAI's CartPole balancing environment
