Mean Shift algorithm from scratch in Python
Welcome to the 41st part of our machine learning tutorial series, and another tutorial within the topic of Clustering..
In this tutorial, we begin building our own mean shift algorithm from scratch. To begin, we will start with some code from part 37 of this series, which was when we began building our custom K Means algorithm. I will add one more cluster/group to the original data. Feel free to add the new data or leave it the same as it was.
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')
import numpy as np
X = np.array([[1, 2],
[1.5, 1.8],
[5, 8 ],
[8, 8],
[1, 0.6],
[9,11],
[8,2],
[10,2],
[9,3],])
plt.scatter(X[:,0], X[:,1], s=150)
plt.show()
colors = 10*["g","r","c","b","k"]
If ran, the code generates:
Just like in the K Means part, this creates obvious groups. With K Means, we even told the machine that we wanted 'k' clusters (2). With Mean Shift, we're expecting that the machine just figures that out on its own, and, for us, we're expecting three groups with the code above.
We will begin our Mean Shift class:
class Mean_Shift:
def __init__(self, radius=4):
self.radius = radius
We will start with a radius of 4, since we can estimate with our dataset that a radius of four makes sense. That's all we need for now in the initialization method. Moving on to the fit method:
def fit(self, data):
centroids = {}
for i in range(len(data)):
centroids[i] = data[i]
Here, we begin with creating starting centroids. Recall the method for Mean Shift is:
- Make all datapoints centroids
- Take mean of all featuresets within centroid's radius, setting this mean as new centroid.
- Repeat step #2 until convergence.
So far we have done step 1. Now we need to repeat step 2 until convergence!
while True:
new_centroids = []
for i in centroids:
in_bandwidth = []
centroid = centroids[i]
for featureset in data:
if np.linalg.norm(featureset-centroid) < self.radius:
in_bandwidth.append(featureset)
new_centroid = np.average(in_bandwidth,axis=0)
new_centroids.append(tuple(new_centroid))
uniques = sorted(list(set(new_centroids)))
Here, we begin iterating through each centroid, and finding all featuresets in range. From there, we are taking the average, and setting that average as the "new centroid." Finally, we're creating a uniques variable, which tracks the sorted list of all known centroids. We use set here since there may be duplicates, and duplicate centroids are really just the same centroid.
To conclude the fit method:
prev_centroids = dict(centroids)
centroids = {}
for i in range(len(uniques)):
centroids[i] = np.array(uniques[i])
optimized = True
for i in centroids:
if not np.array_equal(centroids[i], prev_centroids[i]):
optimized = False
if not optimized:
break
if optimized:
break
self.centroids = centroids
Here we note the previous centroids, before we begin to reset "current" or "new" centroids by setting them as the uniques. Finally, we compare the previous centroids to the new ones, and measure movement. If any of the centroids have moved, then we're not content that we've got full convergence and optimization, and we want to go ahead and run another cycle. If we are optimized, great, we break, and then finally set the centroids attribute to the final centroids we came up with.
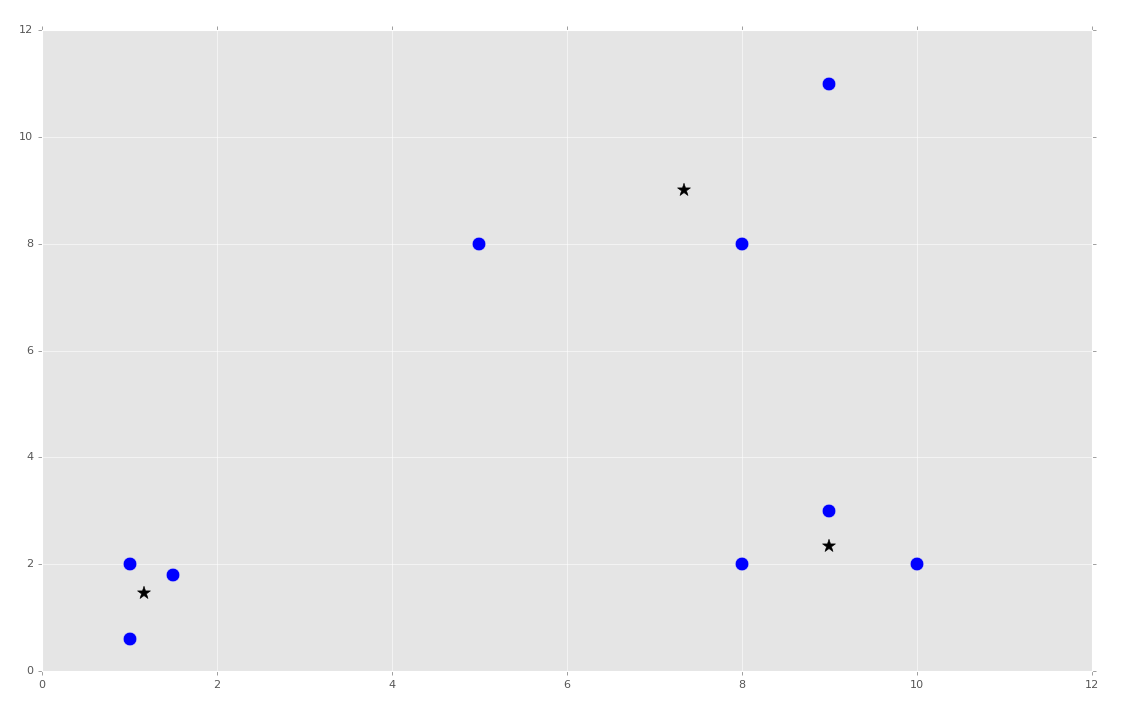
We can now wrap up this first part, and the class, adding the following:
clf = Mean_Shift()
clf.fit(X)
centroids = clf.centroids
plt.scatter(X[:,0], X[:,1], s=150)
for c in centroids:
plt.scatter(centroids[c][0], centroids[c][1], color='k', marker='*', s=150)
plt.show()
Full code up to this point:
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')
import numpy as np
X = np.array([[1, 2],
[1.5, 1.8],
[5, 8 ],
[8, 8],
[1, 0.6],
[9,11],
[8,2],
[10,2],
[9,3],])
##plt.scatter(X[:,0], X[:,1], s=150)
##plt.show()
colors = 10*["g","r","c","b","k"]
class Mean_Shift:
def __init__(self, radius=4):
self.radius = radius
def fit(self, data):
centroids = {}
for i in range(len(data)):
centroids[i] = data[i]
while True:
new_centroids = []
for i in centroids:
in_bandwidth = []
centroid = centroids[i]
for featureset in data:
if np.linalg.norm(featureset-centroid) < self.radius:
in_bandwidth.append(featureset)
new_centroid = np.average(in_bandwidth,axis=0)
new_centroids.append(tuple(new_centroid))
uniques = sorted(list(set(new_centroids)))
prev_centroids = dict(centroids)
centroids = {}
for i in range(len(uniques)):
centroids[i] = np.array(uniques[i])
optimized = True
for i in centroids:
if not np.array_equal(centroids[i], prev_centroids[i]):
optimized = False
if not optimized:
break
if optimized:
break
self.centroids = centroids
clf = Mean_Shift()
clf.fit(X)
centroids = clf.centroids
plt.scatter(X[:,0], X[:,1], s=150)
for c in centroids:
plt.scatter(centroids[c][0], centroids[c][1], color='k', marker='*', s=150)
plt.show()
At this point, we've got the centroids we need, and we're feeling pretty smart. From here, all we need to do is calculate the Euclidean distances, and we have our clusters and classifications! Predictions are easy from there! There's just one problem: The radius
We've basically hard-coded the radius. I did it by looking at the dataset and deciding 4 was a good number. It's not dynamic at all, and this is supposed to be unsupervised machine learning. Imagine if we had 50 dimensions? It wouldn't be so simple. Can a machine look at the dataset and come up with something decent? We'll cover that as well as predictions in the next tutorial.
-
Practical Machine Learning Tutorial with Python Introduction
-
Regression - Intro and Data
-
Regression - Features and Labels
-
Regression - Training and Testing
-
Regression - Forecasting and Predicting
-
Pickling and Scaling
-
Regression - Theory and how it works
-
Regression - How to program the Best Fit Slope
-
Regression - How to program the Best Fit Line
-
Regression - R Squared and Coefficient of Determination Theory
-
Regression - How to Program R Squared
-
Creating Sample Data for Testing
-
Classification Intro with K Nearest Neighbors
-
Applying K Nearest Neighbors to Data
-
Euclidean Distance theory
-
Creating a K Nearest Neighbors Classifer from scratch
-
Creating a K Nearest Neighbors Classifer from scratch part 2
-
Testing our K Nearest Neighbors classifier
-
Final thoughts on K Nearest Neighbors
-
Support Vector Machine introduction
-
Vector Basics
-
Support Vector Assertions
-
Support Vector Machine Fundamentals
-
Constraint Optimization with Support Vector Machine
-
Beginning SVM from Scratch in Python
-
Support Vector Machine Optimization in Python
-
Support Vector Machine Optimization in Python part 2
-
Visualization and Predicting with our Custom SVM
-
Kernels Introduction
-
Why Kernels
-
Soft Margin Support Vector Machine
-
Kernels, Soft Margin SVM, and Quadratic Programming with Python and CVXOPT
-
Support Vector Machine Parameters
-
Machine Learning - Clustering Introduction
-
Handling Non-Numerical Data for Machine Learning
-
K-Means with Titanic Dataset
-
K-Means from Scratch in Python
-
Finishing K-Means from Scratch in Python
-
Hierarchical Clustering with Mean Shift Introduction
-
Mean Shift applied to Titanic Dataset
-
Mean Shift algorithm from scratch in Python
-
Dynamically Weighted Bandwidth for Mean Shift
-
Introduction to Neural Networks
-
Installing TensorFlow for Deep Learning - OPTIONAL
-
Introduction to Deep Learning with TensorFlow
-
Deep Learning with TensorFlow - Creating the Neural Network Model
-
Deep Learning with TensorFlow - How the Network will run
-
Deep Learning with our own Data
-
Simple Preprocessing Language Data for Deep Learning
-
Training and Testing on our Data for Deep Learning
-
10K samples compared to 1.6 million samples with Deep Learning
-
How to use CUDA and the GPU Version of Tensorflow for Deep Learning
-
Recurrent Neural Network (RNN) basics and the Long Short Term Memory (LSTM) cell
-
RNN w/ LSTM cell example in TensorFlow and Python
-
Convolutional Neural Network (CNN) basics
-
Convolutional Neural Network CNN with TensorFlow tutorial
-
TFLearn - High Level Abstraction Layer for TensorFlow Tutorial
-
Using a 3D Convolutional Neural Network on medical imaging data (CT Scans) for Kaggle
-
Classifying Cats vs Dogs with a Convolutional Neural Network on Kaggle
-
Using a neural network to solve OpenAI's CartPole balancing environment
