Percent Change and Correlation Tables - p.8 Data Analysis with Python and Pandas Tutorial
Welcome to Part 8 of our Data Analysis with Python and Pandas tutorial series. In this part, we're going to do some of our first manipulations on the data. Our script up to this point is:
import Quandl
import pandas as pd
import pickle
# Not necessary, I just do this so I do not show my API key.
api_key = open('quandlapikey.txt','r').read()
def state_list():
fiddy_states = pd.read_html('https://simple.wikipedia.org/wiki/List_of_U.S._states')
return fiddy_states[0][0][1:]
def grab_initial_state_data():
states = state_list()
main_df = pd.DataFrame()
for abbv in states:
query = "FMAC/HPI_"+str(abbv)
df = Quandl.get(query, authtoken=api_key)
print(query)
if main_df.empty:
main_df = df
else:
main_df = main_df.join(df)
pickle_out = open('fiddy_states.pickle','wb')
pickle.dump(main_df, pickle_out)
pickle_out.close()
HPI_data = pd.read_pickle('fiddy_states.pickle')
Now we can modify columns like so:
HPI_data['TX2'] = HPI_data['TX'] * 2 print(HPI_data[['TX','TX2']].head())
Output:
TX TX2 Date 1975-01-31 32.617930 65.235860 1975-02-28 33.039339 66.078677 1975-03-31 33.710029 67.420057 1975-04-30 34.606874 69.213747 1975-05-31 34.864578 69.729155
We could have also not made a new column, just re-defined the original TX if we so chose. Removing the whole "TX2" bit of code from our script, let's visualize what we have right now. At the top of your script:
import matplotlib.pyplot as plt
from matplotlib import style
style.use('fivethirtyeight')
Then at the bottom:
HPI_data.plot() plt.legend().remove() plt.show()
Output:
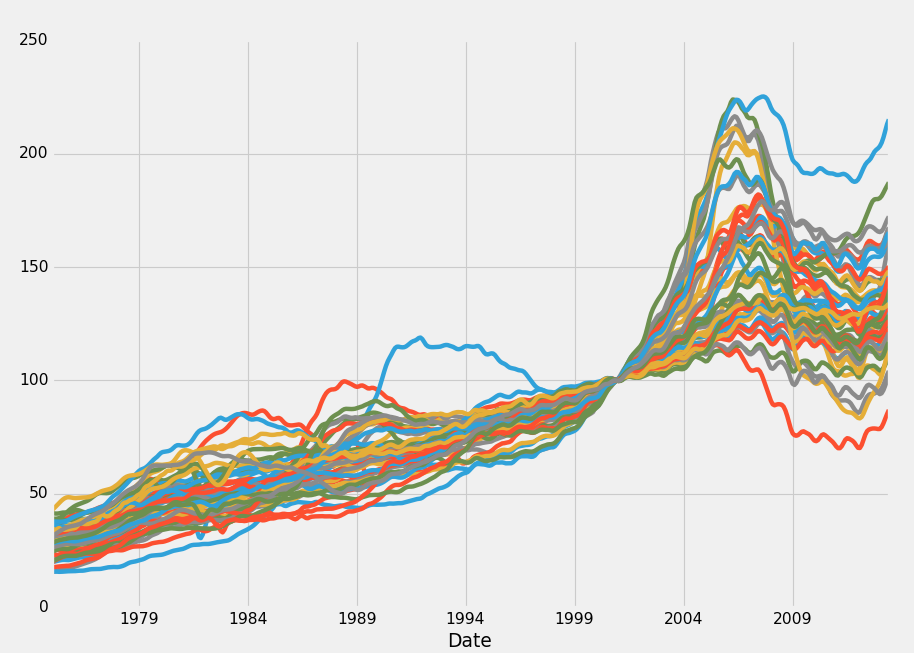
Hmm, interesting, what's going on? All those prices seem to converge perfectly in 2000! Well, this is just when the 100.0% of the index starts. We could get by with this, but I am just simply not a fan. What about some sort of percent change? Turns out, Pandas has you covered here with all sorts of "rolling" statistics. We can slap on a basic one, like this:
def grab_initial_state_data():
states = state_list()
main_df = pd.DataFrame()
for abbv in states:
query = "FMAC/HPI_"+str(abbv)
df = Quandl.get(query, authtoken=api_key)
print(query)
df = df.pct_change()
print(df.head())
if main_df.empty:
main_df = df
else:
main_df = main_df.join(df)
pickle_out = open('fiddy_states2.pickle','wb')
pickle.dump(main_df, pickle_out)
pickle_out.close()
grab_initial_state_data()
Mainly, you are wanting to take note of: df = df.pct_change(), We'll re run this, saving to fiddy_states2.pickle. Notably, we could also attempt to modify the original pickle, rather than re-pulling. That was the point of the pickle, after all. If I didn't have hindsight bias, I might agree with you.
HPI_data = pd.read_pickle('fiddy_states2.pickle')
HPI_data.plot()
plt.legend().remove()
plt.show()
Output:
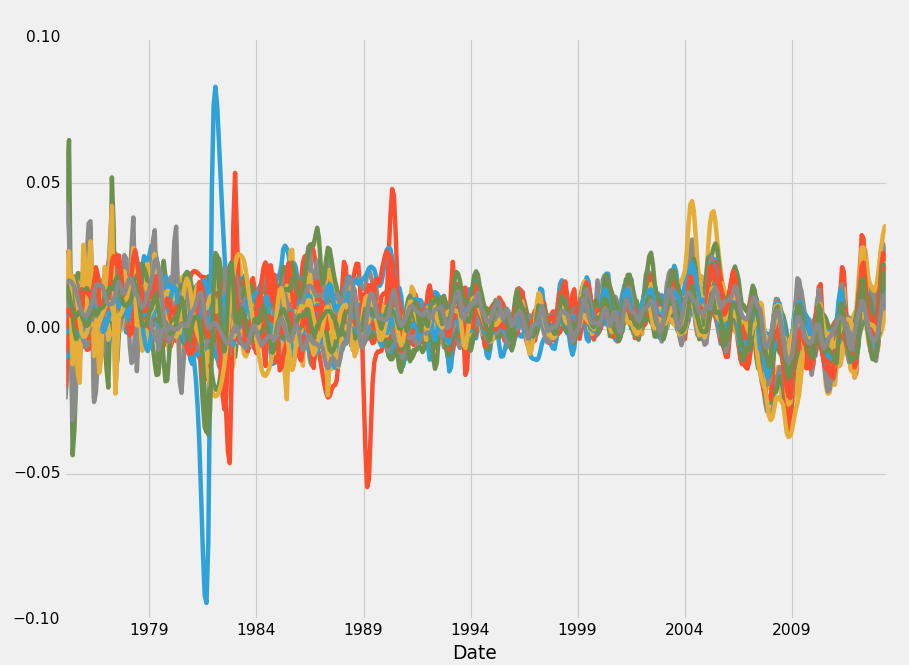
Not quite what I was thinking, unfortunately. I want a traditional % Change chart. This is %change from the last reported value. We could increase it, and do something like a rolling % of the last 10 values, but still not quite what I want. Let's try something else:
def grab_initial_state_data():
states = state_list()
main_df = pd.DataFrame()
for abbv in states:
query = "FMAC/HPI_"+str(abbv)
df = Quandl.get(query, authtoken=api_key)
print(query)
df[abbv] = (df[abbv]-df[abbv][0]) / df[abbv][0] * 100.0
print(df.head())
if main_df.empty:
main_df = df
else:
main_df = main_df.join(df)
pickle_out = open('fiddy_states3.pickle','wb')
pickle.dump(main_df, pickle_out)
pickle_out.close()
grab_initial_state_data()
HPI_data = pd.read_pickle('fiddy_states3.pickle')
HPI_data.plot()
plt.legend().remove()
plt.show()
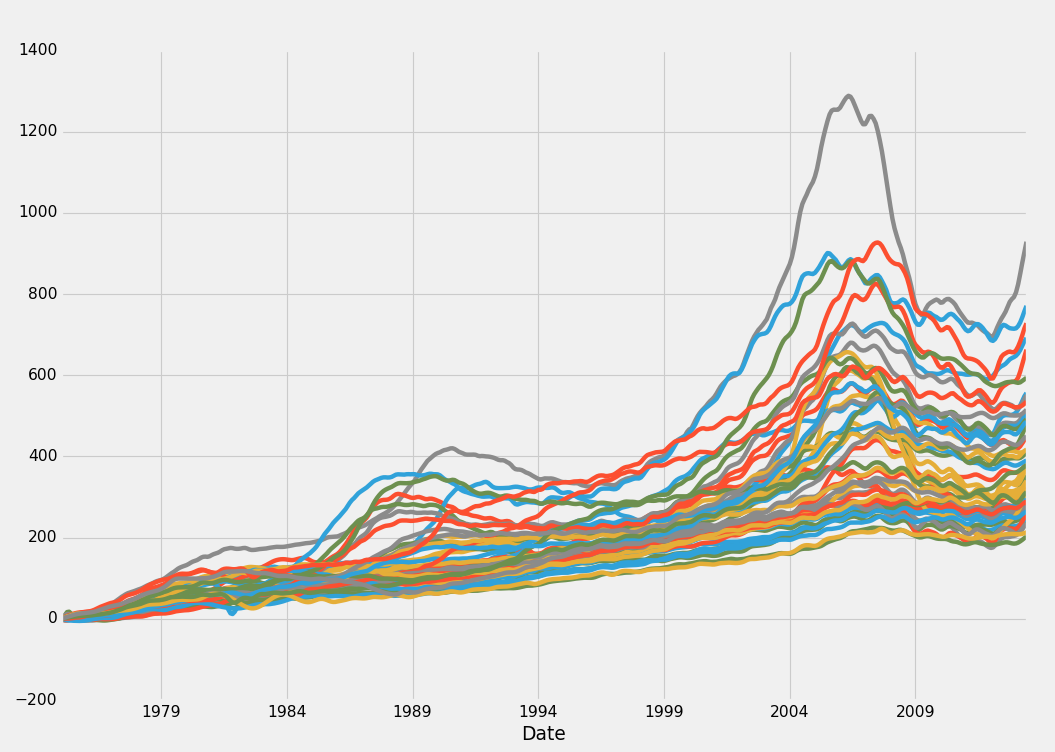
Bingo, that's what I am looking for! This is a % change for the HPI itself, by state. The first % change is still useful too for various reasons. We may wind up using that one in conjunction or instead, but, for now, we'll stick with typical % change from a starting point.
Now, we may want to bring in the other data sets, but let's see if we can get anywhere on our own. First, we could check some sort of "benchmark" so to speak. For this data, that benchmark would be the House Price Index for the United States. We can collect that with:
def HPI_Benchmark():
df = Quandl.get("FMAC/HPI_USA", authtoken=api_key)
df["United States"] = (df["United States"]-df["United States"][0]) / df["United States"][0] * 100.0
return df
Then we'll do:
fig = plt.figure()
ax1 = plt.subplot2grid((1,1), (0,0))
HPI_data = pd.read_pickle('fiddy_states3.pickle')
benchmark = HPI_Benchmark()
HPI_data.plot(ax=ax1)
benchmark.plot(color='k',ax=ax1, linewidth=10)
plt.legend().remove()
plt.show()
Output:
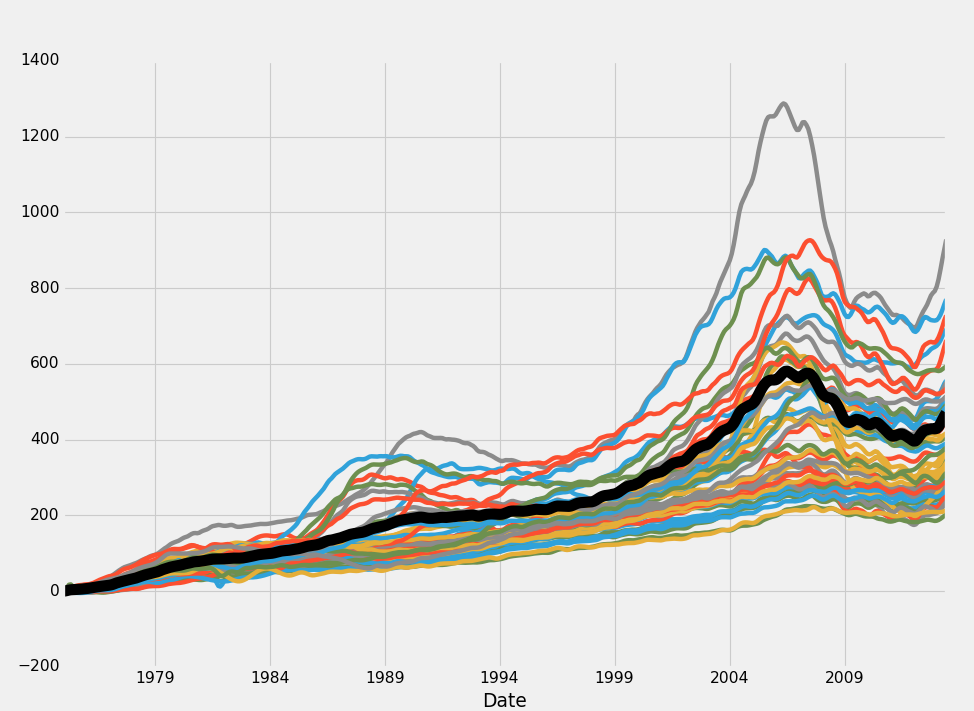
Looking at this data, it appears to be that all markets are relatively closely obeying each other as well as the overall house price index. There does exist some mean deviation here, but basically every market appears to follow a very similar trend. There winds up being quite a major divergence in the end, from 200% increase to over 800% increase, so obviously we have a major divergence there, but the mean is between 400 and 500% growth in the last upper 30 years.
How might we approach the markets possibly? Later on, we could take demographics and interest rates into consideration for predicting the future, but not everyone is interested in the game of speculation. Some people want more safe and secure investments instead. It looks to me here, like the housing markets just never really fail on a state-level. Obviously our plan might fail if we buy a home that later we find out has a major termite infestation and could collapse at any moment.
Staying macro, it is clear to me that we could engage in a very, apparently, safe pair-trading situation here. We can collect correlation and covariance information very easily with Pandas. Correlation and Covariance are two very similar topics, often confused. Correlation is not causation, and correlation is almost always included in covariance calculations for normalizing. Correlation is the measure of the degree by which two assets move in relation to eachother. Covariance is the measure of how two assets tend to vary together. Notice that correlation is a measure to the "degree" of. Covariance isn't. That's the important distinction if my own understanding is not incorrect!
Let's create a correlation table. What this will do for us, is look back historically, and measure the correlation between every single state's movements to every other state. Then, when two states that are normally very highly correlated start to diverge, we could consider selling property in the one that is rising, and buying property in the one that is falling as a sort of market neutral strategy where we're just profiting on the gap, rather than making some sort of attempt to predict the future. States that border each other probably are more likely to have more similar correlations than those far away, but we'll see what the numbers say.
HPI_data = pd.read_pickle('fiddy_states3.pickle')
HPI_State_Correlation = HPI_data.corr()
print(HPI_State_Correlation)
The output should be 50 rows x 50 columns, here's some of the output:
AL AK AZ AR CA CO CT \ AL 1.000000 0.944603 0.927361 0.994896 0.935970 0.979352 0.953724 AK 0.944603 1.000000 0.893904 0.965830 0.900621 0.949834 0.896395 AZ 0.927361 0.893904 1.000000 0.923786 0.973546 0.911422 0.917500 AR 0.994896 0.965830 0.923786 1.000000 0.935364 0.985934 0.948341 CA 0.935970 0.900621 0.973546 0.935364 1.000000 0.924982 0.956495 CO 0.979352 0.949834 0.911422 0.985934 0.924982 1.000000 0.917129 CT 0.953724 0.896395 0.917500 0.948341 0.956495 0.917129 1.000000 DE 0.980566 0.939196 0.942273 0.975830 0.970232 0.949517 0.981177 FL 0.918544 0.887891 0.994007 0.915989 0.987200 0.905126 0.926364 GA 0.973562 0.880261 0.939715 0.960708 0.943928 0.959500 0.948500 HI 0.946054 0.930520 0.902554 0.947022 0.937704 0.903461 0.938974 ID 0.982868 0.944004 0.959193 0.977372 0.944342 0.960975 0.923099 IL 0.984782 0.905512 0.947396 0.973761 0.963858 0.968552 0.955033 IN 0.981189 0.889734 0.881542 0.973259 0.901154 0.971416 0.919696 IA 0.985516 0.943740 0.894524 0.987919 0.914199 0.991455 0.913788 KS 0.990774 0.957236 0.910948 0.995230 0.926872 0.994866 0.936523 KY 0.994311 0.938125 0.900888 0.992903 0.923429 0.987097 0.941114 LA 0.967232 0.990506 0.909534 0.982454 0.911742 0.972703 0.907456 ME 0.972693 0.935850 0.923797 0.972573 0.965251 0.951917 0.989180 MD 0.964917 0.943384 0.960836 0.964943 0.983677 0.940805 0.969170 MA 0.966242 0.919842 0.921782 0.966962 0.962672 0.959294 0.986178 MI 0.891205 0.745697 0.848602 0.873314 0.861772 0.900040 0.843032 MN 0.971967 0.926352 0.952359 0.972338 0.970661 0.983120 0.945521 MS 0.996089 0.962494 0.927354 0.997443 0.932752 0.985298 0.945831 MO 0.992706 0.933201 0.938680 0.989672 0.955317 0.985194 0.961364 MT 0.977030 0.976840 0.916000 0.983822 0.923950 0.971516 0.917663 NE 0.988030 0.941229 0.896688 0.990868 0.912736 0.992179 0.920409 NV 0.858538 0.785404 0.965617 0.846968 0.948143 0.837757 0.866554 NH 0.953366 0.907236 0.932992 0.952882 0.969574 0.941555 0.990066 NJ 0.968837 0.934392 0.943698 0.967477 0.975258 0.944460 0.989845 NM 0.992118 0.967777 0.934744 0.993195 0.934720 0.968001 0.946073 NY 0.973984 0.940310 0.921126 0.973972 0.959543 0.949474 0.989576 NC 0.998383 0.934841 0.915403 0.991863 0.928632 0.977069 0.956074 ND 0.936510 0.973971 0.840705 0.957838 0.867096 0.942225 0.882938 OH 0.966598 0.855223 0.883396 0.954128 0.901842 0.957527 0.911510 OK 0.944903 0.984550 0.881332 0.967316 0.882199 0.960694 0.879854 OR 0.981180 0.948190 0.949089 0.978144 0.944542 0.971110 0.916942 PA 0.985357 0.946184 0.915914 0.983651 0.950621 0.956316 0.975324 RI 0.950261 0.897159 0.943350 0.945984 0.984298 0.926362 0.988351 SC 0.998603 0.945949 0.929591 0.994117 0.942524 0.980911 0.959591 SD 0.983878 0.966573 0.889405 0.990832 0.911188 0.984463 0.924295 TN 0.998285 0.946858 0.919056 0.995949 0.931616 0.983089 0.953009 TX 0.963876 0.983235 0.892276 0.981413 0.902571 0.970795 0.919415 UT 0.983987 0.951873 0.926676 0.982867 0.909573 0.974909 0.900908 VT 0.975210 0.952370 0.909242 0.977904 0.949225 0.951388 0.973716 VA 0.972236 0.956925 0.950839 0.975683 0.977028 0.954801 0.970366 WA 0.988253 0.948562 0.950262 0.982877 0.956434 0.968816 0.941987 WV 0.984364 0.964846 0.907797 0.990264 0.924300 0.979467 0.925198 WI 0.990190 0.930548 0.927619 0.985818 0.943768 0.987609 0.936340 WY 0.944600 0.983109 0.892255 0.960336 0.897551 0.950113 0.880035
So now we can see correlation in HPI movements between every single state pair. Very interesting, and, as is glaringly obvious, all of these are pretty high. Correlation is bounded from -1 to positive 1. 1 being a perfect correlation, and -1 being a perfect negative correlation. Covariance has no bound. Wonder about some more stats? Pandas has a very nifty describe method:
print(HPI_State_Correlation.describe())
Output:
AL AK AZ AR CA CO \
count 50.000000 50.000000 50.000000 50.000000 50.000000 50.000000
mean 0.969114 0.932978 0.922772 0.969600 0.938254 0.958432
std 0.028069 0.046225 0.031469 0.029532 0.031033 0.030502
min 0.858538 0.745697 0.840705 0.846968 0.861772 0.837757
25% 0.956262 0.921470 0.903865 0.961767 0.916507 0.949485
50% 0.976120 0.943562 0.922784 0.976601 0.940114 0.964488
75% 0.987401 0.957159 0.943081 0.989234 0.961890 0.980550
max 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
CT DE FL GA ... SD \
count 50.000000 50.000000 50.000000 50.000000 ... 50.000000
mean 0.938752 0.963892 0.920650 0.945985 ... 0.959275
std 0.035402 0.028814 0.035204 0.030631 ... 0.039076
min 0.843032 0.846668 0.833816 0.849962 ... 0.794846
25% 0.917541 0.950417 0.899680 0.934875 ... 0.952632
50% 0.941550 0.970461 0.918904 0.949980 ... 0.972660
75% 0.960920 0.980587 0.944646 0.964282 ... 0.982252
max 1.000000 1.000000 1.000000 1.000000 ... 1.000000
TN TX UT VT VA WA \
count 50.000000 50.000000 50.000000 50.000000 50.000000 50.000000
mean 0.968373 0.944410 0.953990 0.959094 0.963491 0.966678
std 0.029649 0.039712 0.033818 0.035041 0.029047 0.025752
min 0.845672 0.791177 0.841324 0.817081 0.828781 0.862245
25% 0.955844 0.931489 0.936264 0.952458 0.955986 0.954070
50% 0.976294 0.953301 0.956764 0.968237 0.970380 0.974049
75% 0.987843 0.967444 0.979966 0.976644 0.976169 0.983541
max 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
WV WI WY
count 50.000000 50.000000 50.000000
mean 0.961813 0.965621 0.932232
std 0.035339 0.026125 0.048678
min 0.820529 0.874777 0.741663
25% 0.957074 0.950046 0.915386
50% 0.974099 0.973141 0.943979
75% 0.984067 0.986954 0.961900
max 1.000000 1.000000 1.000000
[8 rows x 50 columns]
This tells us, per state, what the lowest correlation was, what the average correlation was, what the standard deviation is, the 25% lowest, the middle (median / 50%)... and so on. Obviously they all have a max 1.0, because they are perfectly correlated with themselves. Most importantly, however, all of these states that we're seeing here (some of the 50 columns are skipped, we go from GA to SD) have above a 90% correlation with everyone else on average. Wyoming gets as low as 74% correlation with a state, which, after looking at our table, is Michigan. Because of this, we would probably not want to Invest in Wyoming, if Michigan is leading the pack up, or sell our house in Michigan just because Wyoming is falling hard.
Not only could we look for any deviations from the overall index, we could also look for deviations from the individual markets as well. As you can see, we have the standard deviation numbers for every state. We could make attempts to invest in real estate when the market falls below the standard deviations, or sell when markets get above standard deviation. Before we get there, let's address the concepts of smoothing out data, as well as resampling, in the next tutorial.
-
Data Analysis with Python and Pandas Tutorial Introduction
-
Pandas Basics - p.2 Data Analysis with Python and Pandas Tutorial
-
IO Basics - p.3 Data Analysis with Python and Pandas Tutorial
-
Building dataset - p.4 Data Analysis with Python and Pandas Tutorial
-
Concatenating and Appending dataframes - p.5 Data Analysis with Python and Pandas Tutorial
-
Joining and Merging Dataframes - p.6 Data Analysis with Python and Pandas Tutorial
-
Pickling - p.7 Data Analysis with Python and Pandas Tutorial
-
Percent Change and Correlation Tables - p.8 Data Analysis with Python and Pandas Tutorial
-
Resampling - p.9 Data Analysis with Python and Pandas Tutorial
-
Handling Missing Data - p.10 Data Analysis with Python and Pandas Tutorial
-
Rolling statistics - p.11 Data Analysis with Python and Pandas Tutorial
-
Applying Comparison Operators to DataFrame - p.12 Data Analysis with Python and Pandas Tutorial
-
Joining 30 year mortgage rate - p.13 Data Analysis with Python and Pandas Tutorial
-
Adding other economic indicators - p.14 Data Analysis with Python and Pandas Tutorial
-
Rolling Apply and Mapping Functions - p.15 Data Analysis with Python and Pandas Tutorial
-
Scikit Learn Incorporation - p.16 Data Analysis with Python and Pandas Tutorial
