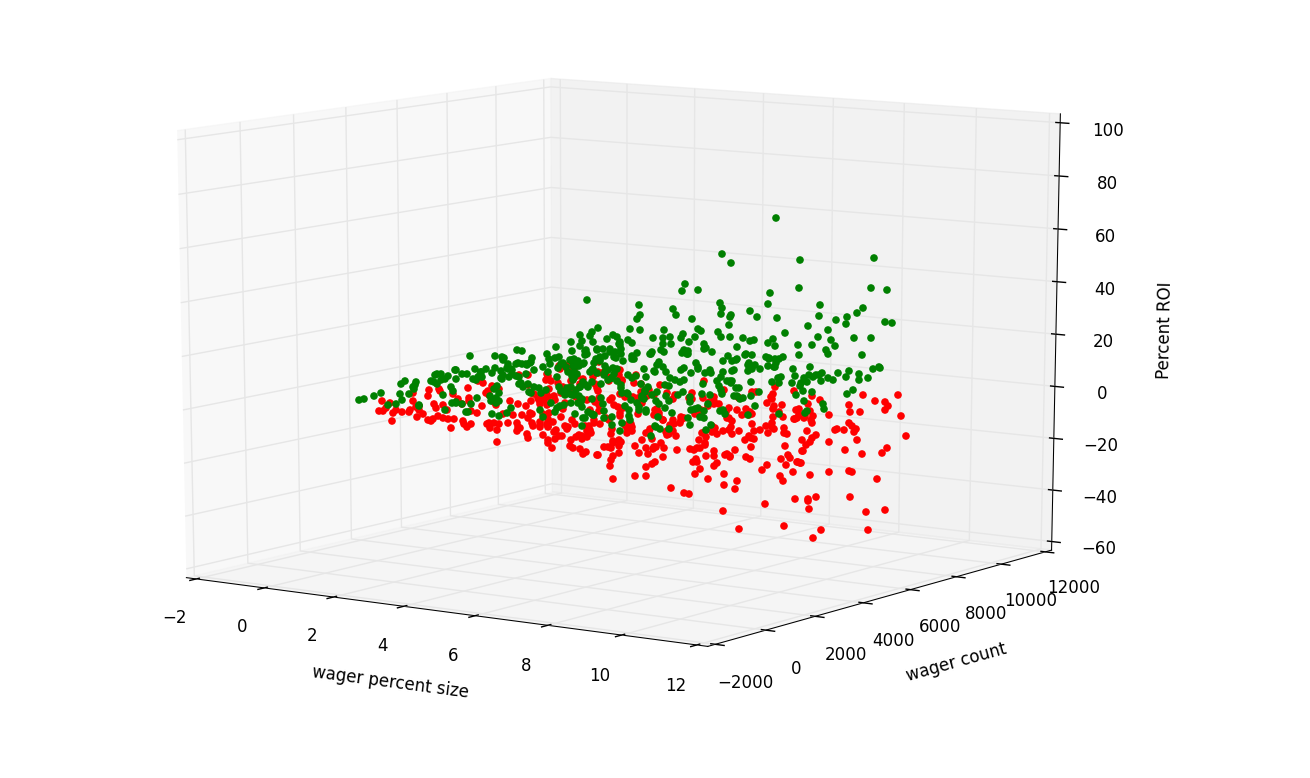
Monte Carlo Simulation and Python
import matplotlib
import matplotlib.pyplot as plt
import csv
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111,projection='3d')
def graph():
with open('monteCarloLiberal.csv','r') as montecarlo:
datas = csv.reader(montecarlo, delimiter=',')
for eachLine in datas:
percentROI = float(eachLine[0])
wagerSizePercent = float(eachLine[1])
wagerCount = float(eachLine[2])
pcolor = eachLine[3]
ax.scatter(wagerSizePercent,wagerCount,percentROI,color=pcolor)
ax.set_xlabel('wager percent size')
ax.set_ylabel('wager count')
ax.set_zlabel('Percent ROI')
plt.show()
graph()

So that's the monte carlo simulator in python. From here, you can use this for all sorts of things. At the end, we searched for variables that gave a result of something greater than something, or less than something. You can also search for vars that give you a range. An example of this is when monte carlo simulations are used to calculate pi. This is done by having the answer, and generating random samples, and selecting the ones that are within a range of the the known answer. From here, we can assume it is close to pi, which it usually is.
We made our simulator, and tested it against a few betting types, trying to find the best strategy, as well as strategy outcomes. Our findings seem plenty obvious to me, however, and that is that there's no way to beat odds to any large degree.
The d'Alembert strategy does do well in terms of steady reliable profit over time, if your wager size is small enough in comparison to your full funds. This means a wager size 1 one millionth of your total funds. In this case, you stand to gain a fraction of a percent of gain on a long term, which will take a very long time to play out, and the earnings would be significant compared to your starting amount.
In the end though, a wager size this small, and the time required to make a profit means you really are just wasting your time with the strategy.
Most people gamble for the excitement either knowingly or unknowingly. A lot of people gamble with the intention to make money. I imagine a few people watched this series and actually heard of the monte carlo strategy because of its relationship with odds and gambling, hoping to learn a new skill to make money. Maybe I'll have saved you some money, but that's the best I have besides teaching you some programming skills.
In the end, gambling should just be for the fun. As soon as you decide to gamble for profit, you are setting yourself up immediately for failure and depression.
The most fascinating part of all of this to me is the degree randomness plays, especially when concerning outliers. The far outliers are heavily influenced by pure randomness in these examples. In today's world, the outliers are often looked towards with either admiration or discontent, depending on which direction they outlie, usually with very little appreciation towards the randomness that played a roll in their path.
I hope you all enjoyed the series, I had fun making it. Like with quite a few of my series, I just made this as I went, so there could very possibly be errors in the code. I encourage you to read it over, test, and develop your own code entirely.
Since we were testing betting strategies in this series, I have since appended another video, covering the Labouchere strategy.
-
Monte Carlo Introduction
-
Monte Carlo dice Function
-
Creating a simple Bettor
-
Plotting Results with Matpltolib
-
Martingale Strategy
-
Bettor Statistics
-
More comparison
-
Graphing Monte Carlo
-
Fixing Debt Issues
-
Analyzing Monte Carlo results
-
Using Monte Carlo to find Best multiple
-
Checking betting results
-
D'Alembert Strategy
-
50/50 Odds
-
Analysis of D'Alembert
-
Comparing Profitability
-
Finding best D'Alembert Multiple
-
Two dimensional charting monte carlo
-
Monte Carlo Simulation and Python
-
Labouchere System for Gambling Tested
