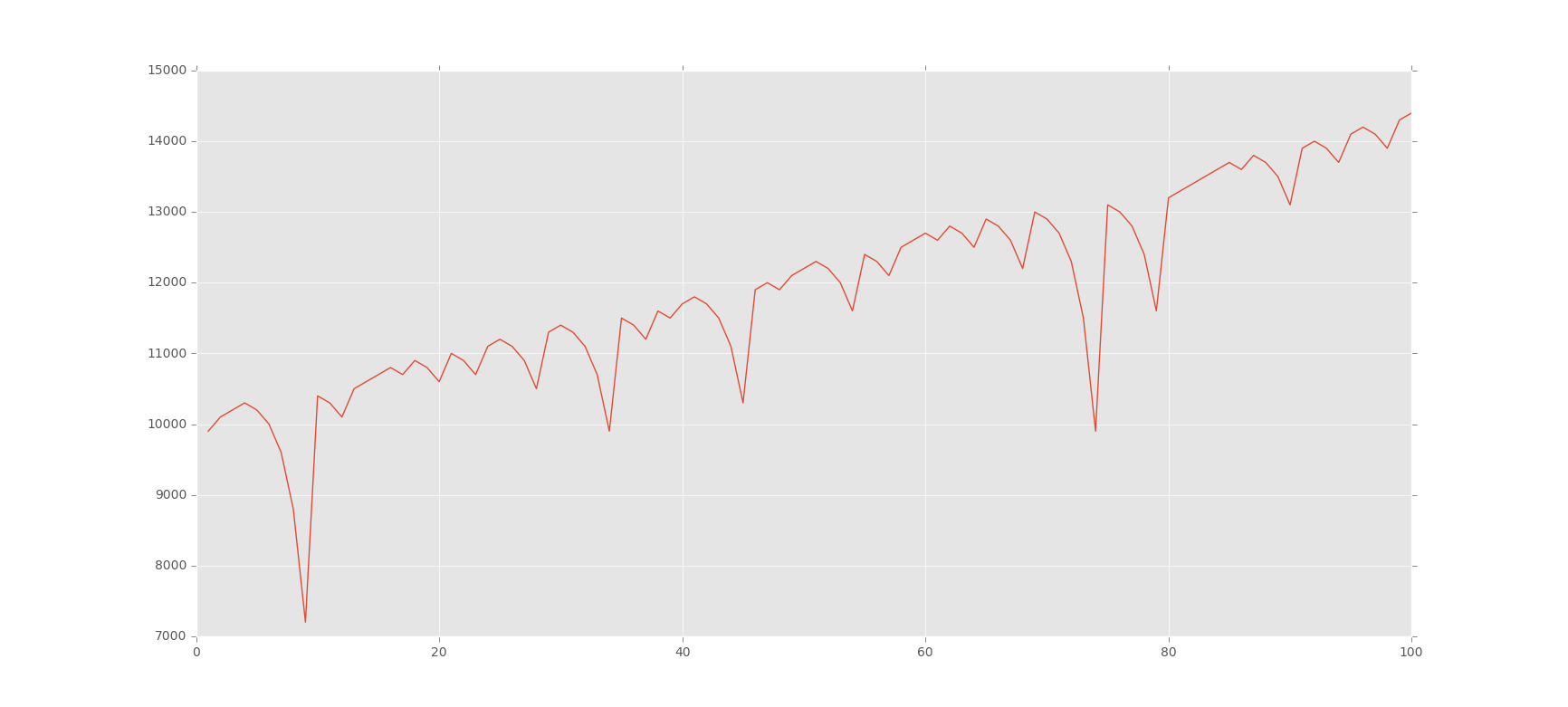
Martingale Strategy

One of the most common bright ideas people get is to double up on losses. Thus, if you lose, you just simply double the previous wager amount. You continue this until a win.

If you have unlimited money, this strategy works, but you don't, so it doesn't. All this strategy does is accelerates the process. Again, each time you wager, you face whatever the odds are. You cannot avoid them. Regardless, we're going to illustrate it!

import random
import matplotlib
import matplotlib.pyplot as plt
#
import time

def rollDice():
    roll = random.randint(1,100)

    if roll == 100:
        return False
    elif roll <= 50:
        return False
    elif 100 > roll >= 50:
        return True


def doubler_bettor(funds,initial_wager,wager_count):
    value = funds
    wager = initial_wager
    wX = []
    vY = []
    currentWager = 1

    # since we'll be betting based on previous bet outcome #
    previousWager = 'win'

    # since we'll be doubling #
    previousWagerAmount = initial_wager

    while currentWager <= wager_count:
        if previousWager == 'win':
            print 'we won the last wager, yay!'
            if rollDice():
                value += wager
                print value
                wX.append(currentWager)
                vY.append(value)
            else:
                value -= wager  
                previousWager = 'loss'
                print value
                previousWagerAmount = wager
                wX.append(currentWager)
                vY.append(value)
                if value < 0:
                    print 'went broke after',currentWager,'bets'
                    currentWager += 10000000000000000
        elif previousWager == 'loss':
            print 'we lost the last one, so we will be super smart & double up!'
            if rollDice():
                wager = previousWagerAmount * 2
                print 'we won',wager
                value += wager
                print value
                wager = initial_wager
                previousWager = 'win'
                wX.append(currentWager)
                vY.append(value)
            else:
                wager = previousWagerAmount * 2
                print 'we lost',wager
                value -= wager
                if value < 0:
                    print 'went broke after',currentWager,'bets'
                    currentWager += 10000000000000000
                print value
                previousWager = 'loss'
                previousWagerAmount = wager
                wX.append(currentWager)
                vY.append(value)
                if value < 0:
                    print 'went broke after',currentWager,'bets'
                    currentWager += 10000000000000000

        currentWager += 1

    print value
    plt.plot(wX,vY)

    
            
            
doubler_bettor(10000,100,100)
plt.show()
time.sleep(555)




'''
Simple bettor, betting the same amount each time.
'''
def simple_bettor(funds,initial_wager,wager_count):
    value = funds
    wager = initial_wager
    wX = []
    vY = []
    currentWager = 1
    while currentWager <= wager_count:
        if rollDice():
            value += wager
            wX.append(currentWager)
            vY.append(value)
        else:
            value -= wager
            wX.append(currentWager)
            vY.append(value)
        currentWager += 1
    plt.plot(wX,vY)
x = 0


while x < 100:
    simple_bettor(10000,100,1000)
    x += 1

plt.ylabel('Account Value')
plt.xlabel('Wager Count')
plt.show()

		

The next tutorial: Bettor Statistics